1. Hàm số y = ax2 (a ≠ 0)
Hàm số y = ax2 (a ≠ 0) : Hàm số xác định với mọi số thực x
Tính chất biến thiên:
+ Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0.
+ Nếu a < 0 thì hàm đồng biến khi x < 0, nghịch biến khi x > 0.
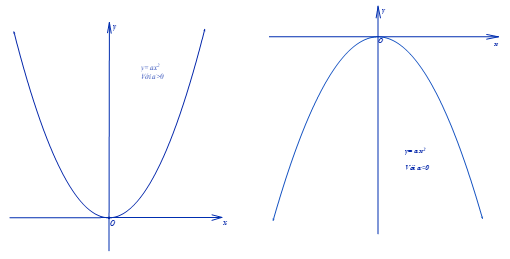
Đồ thị hàm số là một đường Parabol nhận gốc tọa độ O làm đỉnh, nhận trục tung làm trục đối xứng. Khi a > 0 thì Parabol có bề lõm quay lên trên, khi a < 0 thì Parabol có bề lõm quay xuống dưới.
2. Phương trình bậc hai một ẩn
Phương trình bậc hai một ẩn là phương trình có dạng: ax2 + bx + c = 0. Trong đó x là ẩn số; a, b, c là những số cho trước gọi là các hệ số và a ≠ 0.
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và biểu thức Δ = b2 - 4ac.
+ Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt
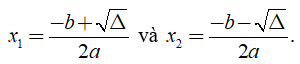
+ Nếu Δ = 0 thì phương trình có nghiệm kép là 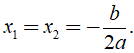
+ Nếu Δ < 0 thì phương trình vô nghiệm.
Đối với phương trình ax2 + bx + c = 0 (a ≠ 0) và b = 2b'; Δ' = b'2 - ac
+ Nếu Δ' > 0, phương trình có hai nghiệm phân biệt
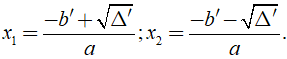
+ Nếu Δ' = 0, phương tình có nghiệm kép là 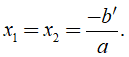
+ Nếu Δ' < 0, phương trình đã cho vô nghiệm.
3. Định lý Vi – ét và ứng dụng
Định lý Viet: Nếu x1, x2 là hai nghiệm của phương trình
ax2 + bx + c = 0, (a ≠ 0) thì
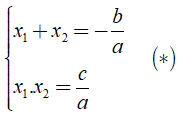
Chú ý: Trước khi sử dụng định lý Viet, chúng ta cần kiểm tra điều kiện phương trình có nghiệm, nghĩa là Δ ≥ 0.
Một số ứng dụng cơ bản của định lý Viet
+ Nhẩm nghiệm của một phương trình bậc hai:
Nếu a + b + c = 0 thì phương trình có hai nghiệm là x1 = 1; x2 = c/a.
Nếu a - b + c = 0 thì phương trình có hai nghiệm là x1 = -1; x2 = -c/a.
+ Tính giá trị của biểu thức g(x1, x2) trong đó g(x1, x2) là biểu thức đối xứng giữa hai nghiệm x1, x2 của phương trình (*):
Bước 1: Kiểm tra điều kiện Δ ≥ 0, sau đó áp dụng định lý Viet.
Bước 2: Biểu diễn biểu thức g(x1, x2) theo S = x1 + x2, P = x1.x2 từ đó tính được g(x1, x2).
Một số biểu thức đối xứng giữa hai nghiệm thường gặp:
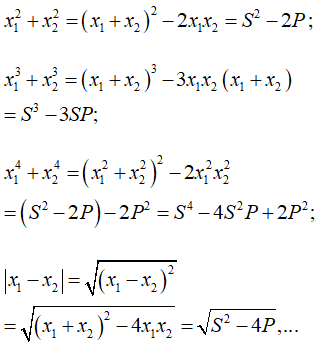
+ Lập phương trình bậc hai có hai nghiệm là x1, x2 cho trước:
⋅ Bước 1: Tính S = x1 + x2; P = x1.x2.
⋅ Bước 2: Phương trình bậc hai nhận hai nghiệm x1, x2 là X2 - S.X + P = 0.
4. Phương trình quy về phương trình bậc hai
a) Phương trình trùng phương
Phương trình trùng phương là phương trình có dạng ax4 + bx2 + c = 0 (a ≠ 0)
Giải phương trình ax4 + bx2 + c = 0 (a ≠ 0)
+ Đặt ẩn phụ x2 = t, t ≥ 0
+ Giải phương trình ẩn phụ mới: at2 + bt + c = 0
+ Với mỗi giá trị tìm được của t, lại giải phương trình x2 = t.
b) Phương trình chứa ẩn ở mẫu
Khi giải phương trình chứa ẩn ở mẫu thức, ta làm như sau:
+ Bước 1: Tìm điều kiện xác định của phương trình
+ Bước 2: Quy đồng mẫu thức hai vế rồi khử mẫu thức
+ Bước 3: Giải phương trình vừa nhận được
+ Bước 4: Trong các giá trị tìm được của ẩn, loại các giá trị không thỏa mãn điều kiện xác định, các giá trị thỏa mãn điều kiện xác định là nghiệm của phương trình đã cho.